TOP100

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6

解析

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function(height) {
    if(height.length < 2) {
        return 0;
    }
    var maxIndex = 0;
    for(var i = 1; i < height.length; i++) {
        if(height[i] > height[maxIndex]) {
            maxIndex = i;
        }
    }
    //双指针,将数组从最高的列分为两段，左边和右边，

    //先找左边能装的水
    var b = 0;
    var water = 0; 
    for(var a = 0; a <= maxIndex; a++) {
        if(height[a] < height[b]) {
            //说明有凹槽，可以接水
            water = water + height[b] - height[a];
        } else {
            b = a;
        }
    }

    //计算右边能装的水
    b = height.length - 1;
    for(var a = height.length - 1; a >= maxIndex; a--) {
        if(height[a] < height[b]) {
            //说明有凹槽，可以接水
            water = water + height[b] - height[a];
        } else {
            b = a;
        }

    }
    return water;

};

本题解法时间复杂度O(N),空间复杂度O(1)

72. 编辑距离

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符 删除一个字符 替换一个字符

解析

/**
 * @param {string} word1
 * @param {string} word2
 * @return {number}
 */
var minDistance = function(word1, word2) {
    //动态规划，dp[i][j]表示word1的前i个单词转换成word2的前j个单词的编辑距离
    //状态转移方程 如果word1[i] != word2[j]: dp[i][j] = Math.min(dp[i- 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1),
    // 如果word1[i] == word2[j]: dp[i][j] = Math.min(dp[i- 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1]),
    var m = word1.length;
    var n = word2.length;
    if(m*n === 0) {
        return m + n;
    }

    var dp = [];
    for(var i = 0; i < m + 1; i++) {
        dp[i] =  new Array(n + 1).fill(0);
    }
    
    //初始化边界
    for(var i = 0; i < m+1; i++) {
        dp[i][0] = i;
    }

    for(var j = 0; j < n + 1; j++) {
        dp[0][j] = j;
    }

    for(var i = 1; i < m + 1; i++) {
        for(var j = 1; j < n + 1; j++) {
            var left = dp[i - 1][j] + 1;
            var down = dp[i][j - 1] + 1;
            var left_down = dp[i - 1][j - 1];
            if(word1[i - 1] !== word2[j - 1]) {
                left_down += 1;
            }
            dp[i][j] = Math.min(left, Math.min(down, left_down));
        }
    }
    return dp[m][n];
};

84 柱状图中最大的矩形

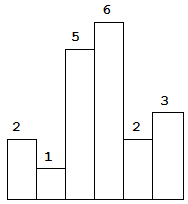
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

解析

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function(heights) {
    //解法一：暴力破解,超出时间限制
    var maxSize = 0;
    var m = heights.length;
    
    for(var i = 0; i < m; i++) {
        for(var j = 0; j <= i; j++) {
            maxSize = Math.max(maxSize, minOfArray(heights.slice(j,i+1))*(i - j + 1) );        
        }
    }

    return maxSize;
};

var minOfArray = function(arr){
    var min = Infinity;
    var QUANTUM = 32768;

    for(var i = 0, len = arr.length; i < len; i+=QUANTUM) {
        var subMin = Math.min.apply(null, arr.slice(i, Math.min(i + QUANTUM, len)));
        min = Math.min(subMin, min);
    }
    return min;
}

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function(heights) {
    //解法二 单调栈
    var n = heights.length;
    var left = new Array(n).fill(0);
    var right = new Array(n).fill(0);
    var stack = [];

    //第一步：求出每根柱子左边最近的小于它高度的柱子
    for(var i = 0; i < n; i++) {
        //将栈顶中高度大于height[i]的元素全部出栈
        while(stack.length != 0 && heights[stack[stack.length - 1]] >= heights[i]) {
            stack.pop();
        }
        //栈顶元素就是i左边最近的低于它高度的索引
        left[i] = stack.length === 0 ? -1: stack[stack.length - 1];
        stack.push(i);
    }

    stack = [];
    //第二步：求出每根柱子右边最近的小于它高度的柱子
    for(var i = n - 1; i >=0 ; i--) {
        //将栈顶中高度大于height[i]的元素全部出栈
        while(stack.length != 0 && heights[stack[stack.length - 1]] >= heights[i]) {
            stack.pop();
        }
        //栈顶元素就是i左边最近的低于它高度的索引
        right[i] = stack.length === 0 ? n : stack[stack.length - 1];
        stack.push(i);
    }

    //第三步：计算结果
    var ans = 0;
    for(var i = 0; i < n; i++) {
        ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
    }
    return ans;


};